Friedlander–Iwaniec theorem
In analytic number theory, an advanced branch of mathematics, the Friedlander–Iwaniec theorem[1] asserts that there are infinitely many prime numbers of the form 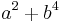 . The first few such primes are
. The first few such primes are
- 2, 5, 17, 37, 41, 97, 101, 137, 181, 197, 241, 257, 277, 281, 337, 401, 457, 577, 617, 641, 661, 677, 757, 769, 821, 857, 881, 977, … (sequence A028916 in OEIS).
The theorem was proved in 1997 by John Friedlander and Henryk Iwaniec,[2] using sieve techniques first developed by Enrico Bombieri.
Iwaniec was awarded the 2001 Ostrowski Prize in part for his contributions to this work.[3]
References
- ^ van Golstein Brouwers, G.; Bamberg, D.; Cairns, J. (2004), "Totally Goldbach numbers and related conjectures", Australian Mathematical Society Gazette 31 (4): 251–255 [p. 254], http://www.austms.org.au/Publ/Gazette/2004/Sep04/Sep04.pdf.
- ^ Friedlander, John; Iwaniec, Henryk (1997), "Using a parity-sensitive sieve to count prime values of a polynomial", PNAS 94 (4): 1054–1058, http://www.pnas.org/content/94/4/1054.abstract.
- ^ "Iwaniec, Sarnak, and Taylor Receive Ostrowski Prize"
Further reading
- Cipra, Barry (1998), "Sieving Prime Numbers From Thin Ore", Science 279 (5347): 31, doi:10.1126/science.279.5347.31.